resultant vector in physics|3.2: Vectors : Cebu A vector is a quantity that has both magnitude and direction. Displacement, . Despite their robust capabilities, PLM systems may not always be the most suitable solution for every manufacturer’s NPI needs as the complexity and costs involved can outweigh the benefits. As a result, many companies are turning to advanced software like Singlepoint to streamline their processes, enhance collaboration, and provide real-time .
resultant vector in physics,The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will be vector R. As shown in the diagram, vector R can be determined by the use of an .
As mentioned earlier in this lesson, any vector directed at an angle to the .A vector is a quantity that has both magnitude and direction. Displacement, .
The resultant vector shows the net force on the object and the direction in which the object will move. What is a Resultant Vector? A vector, which is represented by.To find the resultant vector, simply place the tail of the vertical component at the head (arrow side) of the horizontal component and then draw a line from the origin to the head . This physics video tutorial explains how to find the resultant of two vectors. Full 31 Minute Video on Patreon: / mathsciencetutor Direct Link to The Full Video: https://bit.ly/3ifmore.resultant vector in physicsSolution: From the formula we could say that. \ (\begin {array} {l}\overrightarrow {R}=\sqrt {\overrightarrow {4^ {2}}+\overrightarrow {5^ {2}}}\end {array} \) \ (\begin {array} .Solution: The two vectors are A = 5 units, B = 6 units and the angle Ø = 60°. The resultant vector can be obtained by the following formula. R 2 = A 2 + B 2 + 2ABCosØ. = 5 2 + 6 2 + 2×5×6×Cos60°. = 25 + 36 + 60 × 1/2. = 61 .Draw the resultant from the tail of the first vector to the head of the last vector. Label this vector as Resultant or simply R. Using a ruler, measure the length of the resultant and determine its magnitude by converting to .
The resultant vector, \(\vec r_{tot}\) is drawn from the tail of the first vector to the head of the last vector as shown. Figure 6.1.3: Head-to-Tail Method for Vector Addition. To check this method, let us sum the three vectors . OpenStax. Learning Objectives. By the end of this section, you will be able to: Understand the rules of vector addition, subtraction, and multiplication. Apply .
resultant vector in physics 3.2: Vectors Step 1: link the vectors head-to-tail. Step 2: the resultant vector is formed by connecting the tail of the first vector to the head of the second vector. To combine vectors using the .
The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the magnitude and direction of a resultant vector. The steps to add vectors A and B using the analytical method are as follows: Step 1: Determine the coordinate system for the vectors.The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will be vector R. As shown in the diagram, vector R can be determined by the use of an accurately drawn, scaled, vector addition diagram. (2) Place the vectors head to tail. (3) Draw the resultant vector . (4) Use a ruler and protractor to measure the magnitude and direction of . Figure \(\PageIndex{16}\) In this case, = 23. 0 m and = 7. 5 º south of east. (5) To determine the location of the dock, we repeat this method to add vectors and. We obtain the resultant vector ':If they are in the opposite direction or same direction, then we can add and subtract directly. But they are in the same direction, then we cannot add directly. For a case like this, we use the formula that will square root of the sum of squares of each vector. The resultant vector formula is. \ [\large \overrightarrow {R}=\sqrt .

After rearranging the order in which the three vectors are added, the resultant vector is now the hypotenuse of a right triangle. The lengths of the perpendicular sides of the right triangle are 8.0 m, North (6.0 km + 2.0 km) and 6.0 km, East. The magnitude of the resultant vector (R) can be determined using the Pythagorean theorem.15 m, 210 deg. + 25 m, 300 deg. + 20 m, 45 deg. SCALE: 1 cm = 5 m. When added together in this different order, these same three vectors still produce a resultant with the same magnitude and direction as before (20. m, 312 degrees). The order in which vectors are added using the head-to-tail method is insignificant. Thus, the correct answer is a . More related problems on forces in the AP Physics 1 Exam: AP Physics 1 forces practice problems with MCQs. Problem (7): The magnitudes of two displacement vectors are d d and 2d 2d, and the magnitude of the total displacement is also d\sqrt {3} d 3.
A+B+C = R. Let us have a better understanding of the concept with the help of an example. Example 1. Calculate the resultant vector of three parallel forces pointing upwards. OA = 5N, OB = 10N and OC = 15N. Solution. As we know that the resultant vector is given as: R = OA + OB +OC.

The resultant vector is the vector that 'results' from adding two or more vectors together. There are a two different ways to calculate the resultant vector. Methods for calculating a Resultant Vector: The head to tail method to calculate a resultant which involves lining up the head of the one vector with the tail of the other. The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will be vector R. As shown in the diagram, vector R can be determined by the use of an accurately drawn, scaled, vector addition diagram. Table of Contents .3.2: Vectors Find the resultant vector in form if . Previous Exam Question 3. These questions are provided for practice purposes. There is no guarantee a problem similar to this one will be on your exam. Two vectors each have .For three vectors, for example, we first find the resultant of vector 1 and vector 2, and then we find the resultant of this resultant and vector 3. The order in which we select the pairs of vectors does not matter because the operation of vector addition is commutative and associative (see Equation 2.7 and Equation 2.8 ).
When α = −2, the new vector →C = −2 →A has length C = |−2| A = 3.0 units (twice as long as the original vector) and is antiparallel to the original vector. Figure 3.2.6: Algebra of vectors in one dimension. (a) Multiplication by a scalar. (b) Addition of two vectors ( →R is called the resultant of vectors ( →A and ( →B ).
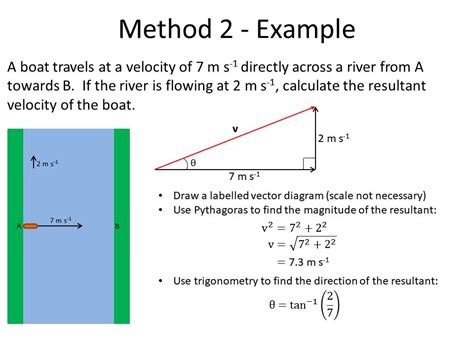
Step 1: Draw a vector diagram. Step 2: Calculate the magnitude of the resultant vector using Pythagoras' Theorem. Resultant vector = 11.66. Step 3: Calculate the direction of the resultant vector using trigonometry. Step 4: State the final answer complete with direction. Resultant vector = 12 km 59° east and upwards from the horizontal. Vectors are essential to physics and engineering. Many fundamental physical quantities are vectors, including displacement, velocity, force, and electric and magnetic vector fields. . For constructing a resultant vector, the parallelogram rule is useful for two vectors while the tail-to-head method is useful for more than two vectors. .
a radial coordinate and an angle. radical coordinate. distance to the origin in a polar coordinate system. resultant vector. vector sum of two (or more) vectors. scalar. a number, synonymous with a scalar quantity in physics. scalar component. a number that multiplies a unit vector in a vector component of a vector.
I review how to find the resultant graphically and then show how to do it algebraically. Suitable for high school physics.How does one add vectors at right angles. Reasonably simple — use pythagorean theorem and tangent. How does one add vectors that aren't at 0°, 180°, or 90°? Brutally simple — resolve them into components. Don't let the vectors make you work harder. Make them point in a direction that's convenient for you. Make them in simpler vectors.
resultant vector in physics|3.2: Vectors
PH0 · What is a Resultant?
PH1 · Vector Addition
PH2 · Resultant Vector Formula
PH3 · Resultant Vector Definition, Formula & Examples
PH4 · How To Find The Resultant of Two Vectors
PH5 · 6.1: Overview of Vectors
PH6 · 3.2: Vectors
PH7 · 3.2: Vector Addition and Subtraction
PH8 · 2.6 Finding the Resultant Vector